 |
|
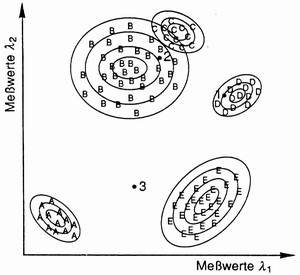
Abb. 7-19: Maximum-Likelihood-Verfahren (aus Albertz, 1991) |
Dieses Verfahren, auch als Verfahren größter Wahrscheinlichkeit bezeichnet, berechnet aufgrund statistischer Kenngrößen der vorgegebenen Klassen die Wahrscheinlichkeiten, mit denen die einzelnen Pixel diesen Klassen angehören. Jedes Pixel wird der Klasse, der es mit der größten Wahrscheinlichkeit angehört, zugewiesen. Dabei wird eine Normalverteilung um den Klassenmittelpunkt angenommen.
Dieses Verfahren ist zwar rechenaufwendig, führt in der Regel aber auch zu guten Ergebnissen, was folgende Abbildung verdeutlicht.
 |
|
Abb. 7-19: Maximum-Likelihood-Verfahren (aus Albertz, 1991) |
Die erhaltenen Standardellipsen sind mit den Rechtecken der Klassifizierungsmethode mittels Quader vergleichbar. Es ist zu erkennen, dass sich die Ellipsen deutlich besser an die Punktwolken annähern als die Rechtecke.
In der Praxis ist die Anwendung der Multispektralen Klassifizierung natürlich komplizierter, da die Anwendbarkeit durch Störfaktoren eingeschränkt wird. Oft unterscheiden sich die spektralen Signaturen der Objektklassen nicht deutlich
genug voneinander, die Punkthaufen überlappen sich.
Selbst eigene Objektklassen sind in sich nicht homogen. Beispielsweise können bei einem Getreidefeld innerhalb der Fläche Unterschiede im Bewuchs und damit in den multispektralen Messwerten auftreten. Bei Siedlungs- und Industrieanlagen ist dies in noch stärkerem
Ausmaß der Fall. Auch Mischsignaturen, d.h. verschiedene Objektklassen,
die von einem Pixel registriert werden, treten auf. Dies passiert beispielsweise an Grenzen zwischen zwei Flächen. Das Geländerelief verursacht bei hügeligem Gelände eine ungleiche Beleuchtung (Schattenseite vs. Sonnenseite), was zu weiteren Inhomogenitäten innerhalb der Multispektraldaten führt.
Insgesamt unterliegt die Multispektrale Klassifizierung einer Vielzahl von Störeinflüssen. Deshalb sind Sorgfalt, Sachkenntnis und praktische Erfahrungen bei der Bearbeitung äußerst wichtig.
|
|
|
Anwendungen ausgewerteter Bilder |
|
|
|
Klassifizierung mittels Quader |